MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [730]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

Na eletrodinâmica quântica, o momento magnético anômalo de uma partícula é uma contribuição dos efeitos da mecânica quântica, expressos pelos diagramas de Feynman com loops, ao momento magnético dessa partícula. (O momento magnético, também chamado de momento de dipolo magnético, é uma medida da força de uma fonte magnética.)

O momento magnético de "Dirac", correspondente aos diagramas de Feynman em nível de árvore (que pode ser pensado como o resultado clássico), pode ser calculado a partir da equação de Dirac. Geralmente é expresso em termos do fator-g; a equação de Dirac prevê $g=2$ . Para partículas como o elétron, esse resultado clássico difere do valor observado por uma pequena fração de um por cento. A diferença é o momento magnético anômalo, denotado por $�$ e definido como

a={\frac {g-2}{2}}

Elétron

A contribuição de um loop para o momento magnético anômalo - correspondente à primeira e maior correção da mecânica quântica - do elétron é encontrada calculando a função de vértice mostrada no diagrama adjacente. O cálculo é relativamente simples ^[1] e o resultado de um loop é:

a_{\text{e}}={\frac {\alpha }{2\pi }}\approx 0.001\,161\,4,

onde $\alpha$ é a constante de estrutura fina. Este resultado foi encontrado pela primeira vez por Julian Schwinger em 1948 ^[2] e está gravado em sua lápide. Em 2016, os coeficientes da fórmula da EDQ para o momento magnético anômalo do elétron são conhecidos analiticamente até $\alpha ^{3}$ ^[3] e foram calculados até a ordem $\alpha ^{5}$ :^[4]^[5]^[6]

a_{\text{e}}=0.001\,159\,652\,181\,643(764)

A previsão da EDQ concorda com o valor medido experimentalmente em mais de 10 algarismos significativos, tornando o momento magnético do elétron a previsão verificada com maior precisão na história da física. (Consulte os testes de precisão da EDQ para obter detalhes.) O valor experimental atual e a incerteza são:^[7]

a_{\text{e}}=0.001\,159\,652\,180\,73(28)

De acordo com este valor, $a_{\text{e}}$ é conhecido com uma precisão de cerca de 1 parte em 1 bilhão (10⁹). Isso exigiu medir $�$ com uma precisão de cerca de 1 parte em 1 trilhão (10¹²).

Múon

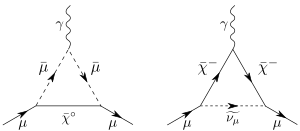
O momento magnético anômalo do múon é calculado de maneira semelhante ao do elétron. A previsão do valor do momento magnético anômalo do múon inclui três partes:^[8]

{\begin{aligned}a_{\mu }^{\mathrm {SM} }&=a_{\mu }^{\mathrm {QED} }+a_{\mu }^{\mathrm {EW} }+a_{\mu }^{\mathrm {hadron} }\\&=0.001\,165\,918\,04(51)\end{aligned}}

Dos dois primeiros componentes, $a_{\mu }^{\mathrm {QED} }$ representa os loops de fótons e léptons e $a_{\mu }^{\mathrm {EW} }$ os loops dos bóson W, bóson de Higgs e bóson Z; ambos os componentes podem ser calculados precisamente a partir de primeiros princípios. O terceiro termo, $a_{\mu }^{\mathrm {hadron} }$ , representa loops de hádrons; ele não pode ser calculado com precisão apenas a partir da teoria. Seu valor é estimado a partir de medições experimentais da razão entre as seções de choque hadrônica e muônica (R) em colisões elétron-antielétron (e⁻–e⁺). Em julho de 2017, observou-se que a medição discorda do Modelo Padrão em 3,5 desvios padrão,^[9] sugerindo que a física além do Modelo Padrão pode estar tendo um efeito (ou que os erros teóricos/experimentais não estão completamente sob controle). Esta é uma das discrepâncias de longa data entre o Modelo Padrão e os experimentos.

O experimento E821 no Brookhaven National Laboratory (BNL) estudou a precessão de múon e antimúon em um campo magnético externo constante enquanto circulavam em um anel de armazenamento confinante.^[10] O experimento E821 relatou o seguinte valor médio:^[8]

a_{\mu }=0.001\;165\;920\;9(6).

Um novo experimento no Fermilab chamado "Muon g−2" usando o ímã do E821 irá melhorar a precisão deste valor.^[11] A coleta de dados começou em março de 2018 e deve terminar em setembro de 2022.^[12] Um resultado provisório divulgado em 7 de abril de 2021^[13] rende $a_{\mu }=0.001\,165\,920\,40(54)$ que, em combinação com as medições existentes, fornece uma estimativa mais precisa $a_{\mu }=0.001\,165\,920\,61(41)$ , excedendo a previsão do Modelo Padrão em 4,2 desvios padrão. Além disso, o experimento E34 no J-PARC planeja iniciar sua primeira tomada de dados em 2024.^[14]

Em abril de 2021, um grupo internacional de quatorze físicos relatou que, usando simulações ab-initio de cromodinâmica quântica e eletrodinâmica quântica, eles conseguiram obter uma aproximação baseada em teoria concordando mais com o valor experimental do que com o valor baseado em teoria anterior que se fundamentava em experimentos de aniquilação elétron-pósitron.^[15]^[16]

Tau

A previsão do Modelo Padrão para o momento de dipolo magnético anômalo do tau é de:^[17]

a_{\tau }=0.001\,177\,21(5),

enquanto o melhor limite medido para $a_{\tau }$ é:^[18]

-0.052<a_{\tau }<+0.013.

MASSA GRACELI RELATIVISTA QUÂNTICA DE CAMPOS.

A relatividade restrita, sendo uma nova teoria sobre dinâmica, estabeleceu novas regras que substituíram as Leis de Newton quando fora do limite clássico, e foram elaboradas, conforme discutido, de forma que se reduzissem a elas quando nos limites onde a mecânica clássica vale. Estas novas leis, mais abrangentes, foram também estabelecidas de forma a tornar não só a dinâmica da matéria como também as leis da dinâmica da energia invariantes à mudança de referencial, leis últimas expressas por um conjunto de equações que constituem ainda hoje o pilar fundamental da teoria eletromagnética clássica, as Equações de Maxwell.^[15]

Dentro deste contexto, nos limites onde as leis da mecânica não valem, o conceito clássico de momento ( ${\vec {P}}=m{\vec {V}}$ ) não se mostra mais associado a uma lei de conservação, e a elaboração de um novo conceito de momento condizente com as leis da relatividade restrita e também com a existência de uma lei de conservação associada levou à definição do que se denomina momento relativístico. O momento relativístico P, que satisfaz conforme definido à citada lei de conservação, é definido por:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {p} ={\frac {m_{o}\,\mathbf {v} }{\sqrt {1-\mathbf {v} ^{2}/c^{2}}}}\,.

Comparando-se estas e várias outras equações da dinâmica relativística com as respectivas equações da dinâmica clássica, tem-se a intuição que se pode derivar as leis da dinâmica relativística substituindo a massa inercial m nas equações para a mecânica clássica pelo que se convencionou chamar massa relativística $M(\mathbf {v} )$ :

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

M(\mathbf {v} )={\frac {m_{o}}{\sqrt {1-\mathbf {v} ^{2}/c^{2}}}}\,.

onde

\mathbf {v}

representa a velocidade da partícula em relação ao referencial (inercial) de análise, e

m_{o}

, a massa de repouso antes definida.

Na equação para a massa relativística vemos que esta massa é explicitamente dependente de sua velocidade, e, visto que maiores valores de velocidade nesta equação implicam maiores valores para a massa relativística, indo esta ao infinito no limite que a velocidade $\mathbf {v}$ do objeto iguala-se à velocidade da luz C, não é incomum encontrar-se pessoas ligadas à área científica dizendo que "a massa aumenta a altas velocidades".

O fato é que, apesar de intuitivo - e de muitas das vezes levar a analogias que podem mostrar-se válidas - uma simples substituição da massa inercial clássica pela massa relativística leva, na maioria das vezes a resultados completamente falsos. Vejamos o que ocorre com a força e com a equação de Newton nesta perspectiva.

A relatividade "herda" a definição de força em sua forma mais abrangente que, junto com a definição do momento relativístico, resulta:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {m_{o}\,\mathbf {a} }{\sqrt {1-\mathbf {v} ^{2}/c^{2}}}}+{\frac {m_{o}\,\mathbf {v} \,(\mathbf {v} \cdot \mathbf {a} )}{c^{2}\,({\sqrt {1-\mathbf {v} ^{2}/c^{2}}})^{3}}}

Notoriamente a força que se observa atuando em um corpo que se move com uma velocidade $(\mathbf {v} )$ não pode ser derivada pela simples substituição da expressão da massa relativística na lei da dinâmica de Newton F=ma. A força na mecânica relativística apresenta duas componentes: uma condizente com a "proposta" de massa relativística, paralela à aceleração apresentada pelo corpo, e outra, que nos diz que há também força na direção da velocidade do objeto, termo que não condiz com a "proposta" e tão menos com a mecânica clássica.

Outra incoerência associada à definição de massa relativística pode ser obtida quando esta é substituída na Lei da Gravitação de Newton. Conforme estruturada, a dinâmica da relatividade restrita estabelece a dinâmica dos corpos e energia apenas em situações completamente isentas de campos gravitacionais, e uma equação para a lei da gravitação não figura dentro do âmbito da relatividade restrita. A associação de uma teoria de gravitação à da relatividade restrita nos leva diretamente à relatividade geral.

Assim, conforme tradução do expresso em Classical Daynamics (Thornton et. al), "Nós preferimos nos reter o conceito de massa como uma grandeza invariante, uma propriedade intrínseca dos corpos. O uso dos dois termos, massa de repouso e massa relativística, é hoje considerado obsoleto. Portanto nós sempre iremos nos referir apenas ao termo massa, o qual equivale à massa de repouso. O uso da massa relativística geralmente conduz a erros ao se usar expressões clássicas.".^[16]

Os conceitos de massa longitudinal e massa transversal.^[17] São muito importantes no estudo das colisões de íons pesados relativísticos e na Física de Hádrons por ser um dos observáveis usados para a dedução sobre uma fase da matéria chamada Plasma de Quarks de Gluons. Esta definição vem da definição de aceleração relativística:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {a} ={\frac {1}{\sqrt {m^{2}+\mathbf {p} ^{2}/c^{2}}}}{\bigl (}\mathbf {F} -\mathbf {v} (\mathbf {v} \cdot \mathbf {F} )/c^{2}{\bigr )}\,.

Esta expressão mostra que de forma geral a aceleração de um partícula depende do ângulo entre a força e a velocidade, e geralmente não tem a direção e o sentido da força. Entretanto há dois casos em que a força tem a mesma direção da aceleração, fornecendo algo parecido com a forma clássica de Newton:

quando a força é paralela à velocidade. Neste caso temos, após algumas operações:

{\frac {F}{a}}=m_{o}({\sqrt {m^{2}+\mathbf {p} ^{2}/c^{2}}})^{3}=m_{l}

e a igualdade à direita define o que se convencionou chamar massa longitudinal m_l uma medida da "inércia" deste corpo - mas apenas nas condições em que a força mostre-se estritamente paralela à velocidade;

quando a força é perpendicular à velocidade. Neste caso temos, após algumas operações:

{\frac {F}{a}}=m_{o}{\sqrt {m^{2}+\mathbf {p} ^{2}/c^{2}}}=m_{t}

e a igualdade à esquerda define o que se convencionou chamar massa transversal m_t , uma medida da "inércia" do corpo neste caso em específico.

Conservação da massa – energia

Equivalência entre massa e energia: em situações onde a mecânica clássica deixa de ser válida a lei clássica da conservação da massa deve ser substituída por uma lei mais geral, a lei da conservação da massa-energia.

A mecânica relativística também herda, além dos já falados, dois outros conceitos bem intuitivos da mecânica clássica: o conceito de trabalho T de uma força, classicamente definido por:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

$T=\int _{0}^{X_{f}}F.dx=\int _{0}^{t_{f}}Fv.dt$ , e que, em mecânica clássica, conduz à definição $T=F.X.\cos {\theta }$ - válida quando se tem uma força F constante formando sempre o mesmo ângulo $\theta$ com o deslocamento - e o teorema da equiparação entre trabalho e variação da energia cinética, $\delta K=T$ .

A fim de se ter uma energia cinética relativística condizente com o teorema da equivalência citado, devemos inserir a força relativística na equação que define trabalho, o que, após alguns cálculos não muito avançados (para quem sabe um pouco de cálculo integral e diferencial - ver Eisberg et.al, Física Clássica), fornece:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

K={\frac {m_{o}\,c^{2}}{\sqrt {1-\mathbf {v} ^{2}/c^{2}}}}\,-m_{o}c^{2}.

Mostra-se também, sem muita complicação, que no limite onde a velocidade v da partícula é negligenciável perto da velocidade c da luz, a equação da energia cinética relativística se reduz à equação da energia cinética clássica

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

////// $K={\frac {m_{o}v^{2}}{2}}$ .

A equação da energia cinética relativística, assim definida, é uma equação em que há duas parcelas, um dependente de velocidade V do lado esquerdo, e uma independente de V, fixa uma vez conhecida a massa inercial da partícula, do lado direito:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

////// $K=E(V)-E'(0)$ . Transpondo os termos temos

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

////// $E(V)=K+E'(0)$ , e lembrando que a energia total de uma partícula é a soma entre sua energia cinética e demais tipos de energia que esta possui, a intuição nos leva diretamente à conclusão que o termo

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E(\mathbf {v} )={\frac {m_{o}\,c^{2}}{\sqrt {1-\mathbf {v} ^{2}/c^{2}}}}

deve ser interpretado como a energia relativística total da partícula. Quando a velocidade da partícula é nula, sua energia total vale, assim:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E_{(0)}=m_{o}C^{2}

que é a famosa equação de Einstein para a equivalência entre massa e energia.

A validade desta equivalência entre massa de repouso e energia de repouso no contexto da relatividade restrita encontra suporte experimental em uma série de eventos que vão desde a produção e aniquilação de pares de partícula-antipartícula, onde massa de repouso é claramente convertida em energia pura (radiação eletromagnética: raios gama), até reações nucleares onde a conversão de massa de repouso em energia é responsável por manter reatores funcionando, e também por permitir que se construam bombas muito pequenas perto do seu imenso poder de destruição (bombas nucleares).

A energia relativística também obedece, como é de se esperar, a uma lei de conservação: a lei da conservação da massa-energia no contexto da relatividade restrita.

Pesquisar este blog

MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [730]

Elétron

Múon

Tau

Conservação da massa – energia

Comentários

Postar um comentário

Postagens mais visitadas deste blog